

Met deze breuken rekenmachine kun je breuken optellen, aftrekken, vermenigvuldigen en delen. De calculator werkt als volgt:
Deze calculator geeft de uitkomst én de uitwerking van de ingevoerde som.
Tip: Als je een som met breuken niet begrijpt kun je hem door de rekenmachine laten uitrekenen en daarna de "Stap voor Stap" uitwerking bestuderen.
In deze rekenmachine kun je breuken met en zonder helen invoeren.
 Breuk met hele
Breuk met hele Breuk zonder hele
Breuk zonder hele Geheel getal
Geheel getalDe rekenmachine accepteert ook negatieve getallen. Hieronder een aantal voorbeelden van toegestane invoeren met negatieve getallen.
 Negatieve samengestelde breuk
Negatieve samengestelde breuk Negatieve breuk
Negatieve breuk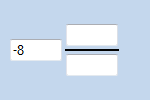 Negatief getal
Negatief getalBij het optellen van breuken is het van belang of de breuken gelijknamig of ongelijknamig zijn. Als de op te tellen breuken gelijknamig zijn, dan geldt voor de uitkomst:
teller = som van de tellersVoorbeeld: 2/4 + 1/4
noemer = noemer van de op te tellen breuken
Als de op te tellen breuken ongelijknamig zijn, moeten ze eerst gelijknamig worden gemaakt.
Voorbeeld: 1/2 + 1/3Breuken van elkaar aftrekken werkt bijna hetzelfde als breuken bij elkaar optellen. Het enige verschil is dat tellers nu niet moeten worden opgeteld maar van elkaar moeten worden afgetrokken.
Het product van 2 of meer breuken, is een breuk waarvoor geldt:
teller = product van de tellersVoorbeeld: 3/2 × 5/2
noemer = product van de noemers
Dus: 3/2 × 5/2 = 15/4
De uitkomst als samengestelde breuk: 3 3/4
Om het product van samengestelde breuken op deze manier uit te kunnen rekenen, moet je ze eerst als gewone breuken schrijven.
Voorbeeld: 3 1/4 × 2 1/23 1/4 × 2 1/2 =
13/4 × 5/2 =
65/8 =
8 1/8
In plaats van bovenstaande berekening kun je er ook voor kiezen om de samengestelde breuken te schrijven als som van helen(n) en een gewone breuk. Daarna kan je dan de haakjes wegwerken en vervolgens het resultaat verder uitwerken.
3 1/4 × 2 1/2 =Uit beide berekeningen blijkt: 3 1/4 × 2 1/2 = 8 1/8
(3 + 1/4) × (2 + 1/2) =
3×2 + 3×1/2 + 1/4×2 + 1/4×1/2 =
6 + 3/2 + 2/4 + 1/8 =
6 + 1 1/2 + 1/2 + 1/8 =
8 + 1/8 =
8 1/8
De uitkomst van een deling met een breuk kun je vinden met behulp van de volgende regel:
delen = vermenigvuldigen met het omgekeerdeVoorbeeld: 2/5 ÷ 4/3
2/5 ÷ 3/4 =Dus: 2/5 ÷ 3/4 = 8/15
2/5 × 4/3 =
8/15